Q. 페르미 에너지 준위에 대해서 설명을 해주세요.
A. 에너지 밴드 그림에서 가운데에 있는 거요!
탈락
전 포스팅에서 양자 역학의 기본과 이를 응용하여 고체 및 Si 반도체로 확장시켰습니다.
이를 통해 에너지 밴드, 가전자대, 전도대, 에너지 밴드갭이 만들어짐을 확인하였죠.
'페르미 에너지 준위의 정의'를 알기 위해 기본적인 사전 지식이 필요합니다.
정말 쉽게 말씀드릴 테니 잘 이해해 주세요.
상태 밀도 함수
상태 밀도 함수의 정의는 '결정의 단위 부피당 차지 가능한 양자 상태 수'입니다.
쉽게 말씀드리면, 전자, hole이 들어갈 수 있는 방(Energy state)입니다.


gc(E)는 전도대의 에너지 상태 밀도 함수, 전자가 들어갈 수 있는 방을 말합니다.
(Valence band에서는 전자는 이미 꽉 차 있죠.)
gv(E)는 가전자대의 에너지 상태 밀도 함수, 정공이 들어갈 수 있는 방을 말합니다.
Conduction band에서 정공은 이미 꽉 차 있죠.)
보시다시피, 밴드갭에는 전자, hole이 들어갈 수 있는 방이 없습니다.
Fermi-Dirac 확률 함수
결정격자 내에서 전자가 존재할 확률입니다.
1에서 Fermi-Dirac 확률 함수를 빼면 정공이 존재할 확률이겠지요.

가로축은 에너지, 세로축은 확률입니다. 시계방향으로 그래프를 돌려볼까요?

파란색, 0K 부분에서는 '수평'입니다. 열을 받으면서 점차적으로 휘어짐을 알 수 있습니다.
에너지를 받은 전자는 더 위에 있는 '방'을 들어가기 더 쉬워집니다.
이 개념을 활용하여 서론에 말씀드렸던, 페르미 에너지 준위에 대해서 설명을 해드리겠습니다.
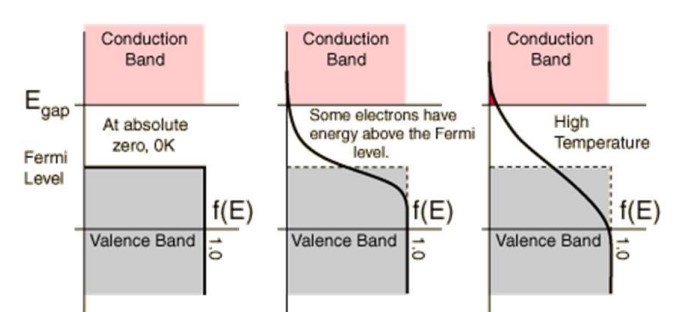
절대온도 0K일 때 전자가 가질 수 있는 최대 에너지인 지점입니다.
절대온도 0K 이상일 때, 전자가 있을 확률이 50%인 지점입니다. (Fermi-Dirac 확률 함수가 50%인 지점)
전자 농도, 정공 농도
상태 밀도 함수와 Fermi-Dirac 확률을 곱하면 실제 캐리어들의 수와 밀도를 구할 수 있습니다.
즉, 전자 농도와 정공 농도를 구할 수 있죠.

그림의 오른쪽 부분을 보시면, 전자 농도, 정공 농도를 구할 수 있음을 알 수 있습니다.
위 사진은 n, p 농도가 같은 '진성 반도체'입니다.
상온은 0K가 아니기 때문에, Fermi-Dirac 곡선이 휘어져 있으며, 50% 되는 지점에서 페르미 에너지 준위가 있음을 확인할 수 있습니다.
Q. 에너지 밴드갭 부분에서는 왜 농도가 없을까요?
'반도체 공학 > 반도체 물성 이론' 카테고리의 다른 글
| 반도체 물성과 소자) 6. 비평형 과잉캐리어 (0) | 2022.10.21 |
|---|---|
| 반도체 물성과 소자) 5. 캐리어 이동 현상(GaAs가 Si보다 빠른 이유), Drift 전류, Carrier 확산 (0) | 2022.10.20 |
| 반도체 물성과 소자) 4. 평형 상태의 진성 반도체, 외인성 반도체의 거동 및 전자, 정공 농도(p형과 n형 도핑 원소를 왜 B(붕소), P(인)을 사용할까?) (0) | 2022.10.19 |
| 반도체 물성과 소자) 2. 고체 양자 이론(feat. 파울리 배타 원리, 에너지 밴드 형성) (0) | 2022.10.17 |
| 반도체 물성과 소자) 1. 양자 역학 입문, 양자 역학을 배우는 이유 (0) | 2022.10.17 |





댓글